Modeling Telephony Hybrids using 2 x 2 Matrices
Author: Douglas Rice
Copyright Douglas Rice, doug.h.rice@btinternet.com , 2005,2008,2015
Further Notes
The theory in this web page draws on information in [1] and [10]. In 1984 a problem with using an EMC filter inserted in a telphone line prompted me to dig out my University course notes on modelling filters using ABCD parameters. For ABCD parameters see [11]. A search of the local reference library did not come up clear diagrams of the impedance looking into the EMC filter. [8] explains some of this. Over a large number of evenings, I used my Nascom 2 computer to write some Pascal to calculate the input impedance of the EMC filter. [1] was a good paper that described how to model Telephone exchanges using ABCD parameters. It was thought too complicated to write Pascal for the equations. The equations for the ABCD model are quite complicated.
(C) permission requested and granted. mar 2017
It occurred to me that I could break the Telephone exchange into three 2x2 matrices, which made the Pascal much simpler.
With the rise of the Internet, Wikipedia, and search engines, I concluded my use of ABCD parameters did not appear elsewhere. After 21 years, I decided to put my web page on my website. In 2009, I ported the Pascal code to JavaScript. 30 years on it would be of interest to record this. The JavaScript and Flot Graps allows me to animate the graphs for different Telephone line lengths. Things of interest are what is the impeadance looking into the Telephone line. What is the Sidetone for different lines lengths. Sidetone is how much does the Talker hear of their own voice, so the Ration E/M is of interest. What value of =Zb is required. =Zb is my notation for equalZb which is the balance impedance, which is the impedance required to give minimun side tone.
References
[1] P K Webb Post Office Research Department Report 630, Computation of the Characteristics of Telephone Connections,1977. [2] R Smith J W Cook, An Integrated Circuit For Analogue Line Interfaces With adaptive Transmission And Extra Facilities, Br Telecom Technology J Vol 5 No 1 January 1987, setion 4 page 36-37. [3] D V Mercy, Phase From Amplitude, Electronics and Wireless World, June 1988 Vol 94 Number 1628. [4] D.V Mercy, Amplitude From Phase, Electronics and Wireless World, July 1988 Vol 94 Number 1629.. [5] BP0 603 [7] D.L Richards, Telecommunication By Speech, Butterworths,1973 [8] F.F. Kuo, Network Analysis and Synthesis, Wiley International,1962 [9] N.A Pashtoon,Chap 4 of D.F.EIIiott, Handbook of Digital Signal Processing Engineering Applications,Academic Press, 1987 [10] Course notes - Sheffield University [11] https://en.wikipedia.org/wiki/Two-port_network [12] http://www.electrical4u.com/abcd-parameters-of-transmission-line/ [13] Flot - FLOT charts [14] BT's SIN 351 Issue 4.6,April 2014 and 352 ( 08/12/2015 ) [15] BT's SIN site for SIN 351 Issue 4.6,April 2014 and 352
Examples - Phone + Artificial Line + Termination. Still in update
In real life Phone use balanced signals, these models are unbalanced, but are still valid.[14] publishes two terminations, but not =Zb.
The Test Circuit:
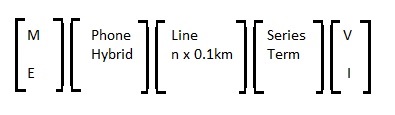
converted to

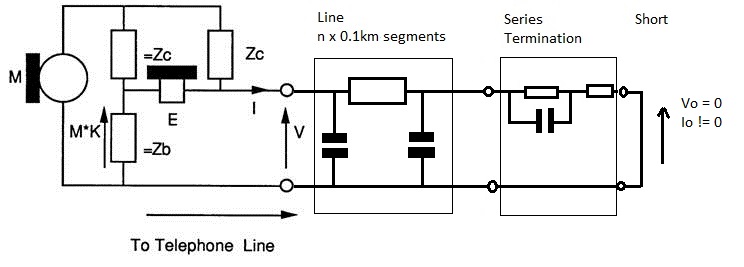
V is a function of M. Using the Series Termination and short V can be made to be 0.
Use Shunt Termination when you need Io =0 and Vo != 0
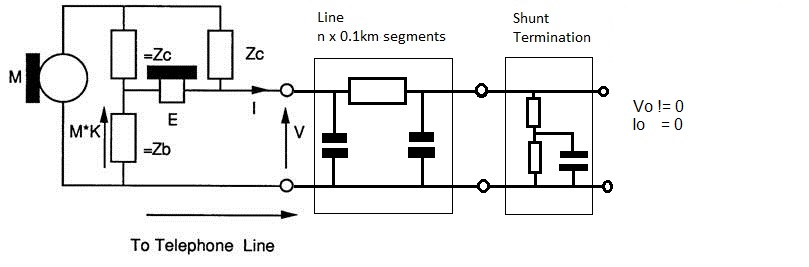
Use Series Termination when you need Vo =0 and Io != 0
a_artline Impedance looking into the Artifical line presented to Phone.
a_artline4W.htm Side Tone Loss. E/M for circuit above. Note Zb is not specified in [14]
a_artline4Wnew.htm Side Tone Loss. E/M for circuit above. Note Zb is not specified in [14]
a_artlineZb.htm Calculating Zterm for zero Side tone. Not really a useful thing to know.
a_inc_32_zc_zn_32.htm Test using Zc, Zn, Zso and Working out Loundess Ratings
Examples - End to End connections - Still in update
You can explore the effect of delay and line length. Set the Loss across the exchange to a large to isolate the effect of the far end line.
The animation can be used to appreciate how the line length or delay affects the sidetone or input impeadance.
Convert() is used to get one of A, B, C or D into a useful value, like Vin = D Iin. leaving the other 3 without and obvious meaning
a_424L424.htm Modelling End To End
a_24L42.htm Looking into Line with exchange and line and termination.
It is Easy to be confused!
ABCD parameters work out inputs using outputs, so you can append from left to right. Also, Iout - is it pointing out or in? Easy to be confused!
Below is a definition of the two port network and the ABCD parameters.
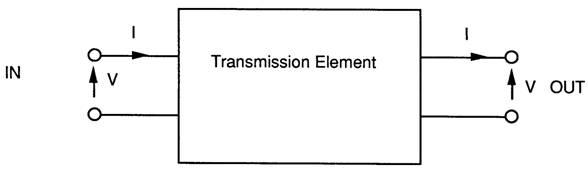
ABCD Matrix representation.
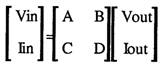
Once a program has been written to chain these together the impedance looking into the network can be calculated as shown below:
Zin=Vin/lin and Vout = ZIoad * lout.
inputs = [ ] outputs The outputs become the inputs of the next stage. inputs = [ 1 ][ 2 ][ 3 ][ 4 ] outputs outputs = [ 4 ][ 3 ][ 2 ][ 1 ] inputs
My function name twoto4( ) could be better named. You calculate the 4 wire M and E using the two wire V and I but the flow is from 4 wire to 2 wire.
// Phone
/*
This models the hybrid inputing 4 wire to 2 wire [ M ] = [ ] [V]
see paper on loudness ratings [ E ] [ ] [I]
*/
twoto4(z_complex_z.r,z_complex_z.i, z_complex_znom.r,z_complex_znom.i );
PROCEDURE twoto4(zcr,zci,zbr,zbi:REAL);
{This models the hybrid inputing 4 wire to 2 wire [ M ] = [ ] [V]
see paper on loudness ratings [ E ] [ ] [I] }
My function name fourto2( ) could be better named. You work out 2 wire V and I using 4 wire M and E.
PROCEDURE fourto2(zcr,zci,zbr,zbi:REAL);
{This models the hybrid inputing 2 wire to 4 wire [ V ] = [ ] [ M ]
[ I ] [ ] [ E ] }
Other notes
Alternative circuits
thevenin's theorem - voltage source in series with Zc
Norton's theorem - current source in parallel with Zc
A voltage source is low impedance. So I := V / Z
A current source is High impedance. So V := I * Z
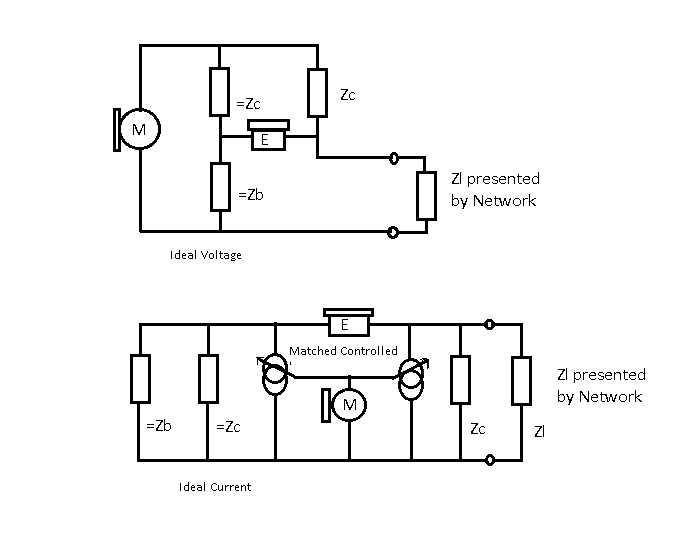
The alternative circuit could use the =Zc and =Zb across the Mic
This simplified circuit is based on a phone schematic:
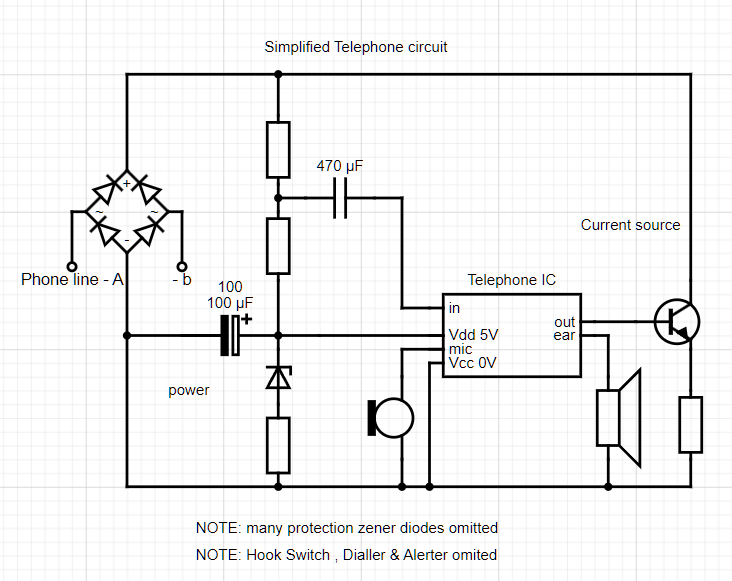
It drives the line using the Norton Equivalent circuit. Controlled Current source in parallel with Zc
This simplified circuit uses an IC powered from the line current.
OUT drives a voltage controlled current source.
There is a resistor across the line, it acts as Zc.
IN taps the middle of of Zc, needed for the Hybrid , K & =Zb, =Zc
The schematic used many protection diodes and dc blocking capacitors, which have been omitted to simplicy the diagram
Note: diagram drawn using https://www.circuit-diagram.org/editor/
Terminal Impedance
See [14]SIN351 3.4.1. Terminal Input Impedance
The impedance necessary to satisfactorily terminate the BT network interface at the NTP so as to prevent instability is represented by the three-element network shown in Figure 1. A minimum return loss of 12 dB should be achieved by terminal equipment against the three-element network of Figure 1.
--[370R]--+--[620R]--+--
| |
+----||----+
310nF
Network Impedance
See [14]SIN351 3.4.2. Network Input Impedance The input impedance of the network at the NTP is represented by a range of impedances comprising the input impedance of the local exchange, modified by the impedance of a random variety of local cable types/characteristics. The nominal exchange input impedance is 300R + 1000R || 220 nF
--[300R]--+--[1000R]--+--
| |
+----||----+
220nF
This may be regarded as the appropriate value for use by terminal designers. NOTE: It can be shown that this is about Zterm + 2km of artificial line, using a_artline Impedance looking into the Artifical line presented to Phone.
What is the impedance presented to the Terminal?
Consider a terminal connected to the Network at the Network Termination Point , NTP.
[terminal]---+---[ line ]---[exchange]
NTP
What is the Zc of the Terminal?
What is the Zc of the Exchange?
What is the Z looking into the line towards the Exchange at the NTP?
What is the Z looking into the line towards the Terminal at the Exchange?
Make Zc of the exchange and Terminal, the Terminal Impedance below:-
--[370R]--+--[620R]--+--
| |
+----||----+
310nF
When you have 2km of line, the Z looking into the line terminated by the network above, the network below is a reasonable fit to:
--[300R]--+--[1000R]--+--
| |
+----||----+
220nF
2km is a reasonably typical line length from the exchange to the Terminal.
We end up with:
[ Zc ] ---+--- [ Line ] --- [ Zc ]
If you make the balance impedance , "==Zb", equal to the Network Impedance, then the Sidetone is quieter at long lines.
The caller's Sidetone will be quieter, so they speak louder.
They speak quieter when there is more sidetone.
When a caller speaks, they hear their own voice, and this is via the jaw bone and via the air path.
I remember STMR meaning "SideToneMaskedRating".
[terminal]---+---[ line ]---[exchange]
NTP
<- Zc <-Zn
Zn-> Zc->
So try setting the balance impedance Zb equal to Zn so Side tone is quietest at 2km.
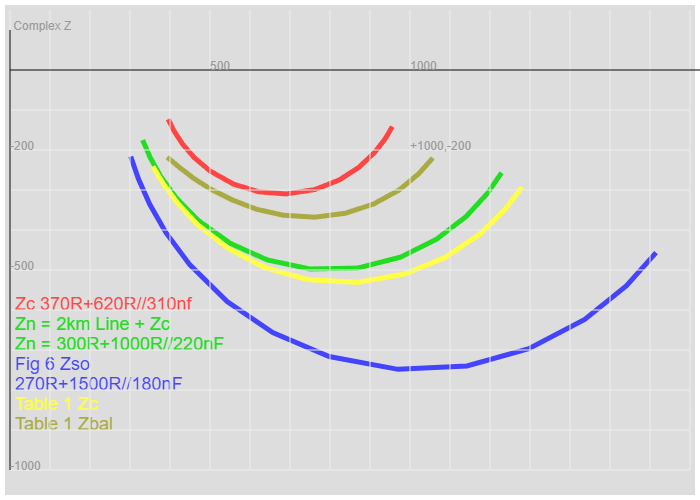
Measuring Zc and return loss
The BTR states the match of Zc to the 370+620//310nf in terms of Return Loss. It assumes the term Return Loss is understood.
"With the 4-wire return path disabled, the input impedance of the exchange port shall be such that the return loss against the the network 370+620//310nf shall be greater than the limit shown"
"Alternatively the input impedance shall be such that the return loss with respect to 600 ohm shall be greater than 18dB over the range 500-3400Hz and 14dB over the range 300-499Hz"
For a Co-Ax, the return loss is very high when Zterm = Zo,
I have forgotten the formulae for Return Loss in terms of Zc
"return loss is a measure in relative terms of the power of the signal reflected"
Return Loss is 20 log( magnitude((Zo-Zterm) / (Zo+Zterm) )
Return Loss is 20 log( magnitude( E / M ) ) , need to check if you use 2E/M and E/M
=Zc and =Zb are made equal so K = 0.5, and Zc is adjusted to Null E
It is easier to find a variable R than a variable C, so adjust =Zc and =Zb to null E/M
Zc,Zb and SIN351 and SIN355
My paper was written 30 years ago, and well before SIN351 and SIN355.
My paper writes about Zc, the Input impedance and output Impedance for the Hybrid.See[8]
The Balance impedance is the impedance that, connected across the terminals, would give zero side tone.
The Phone circuit is like a Wheatstone bridge. The Microphone voltage M drives the bridge and the Earphone is the detector.
When Zb/(Zc+Zb) == (=Zc/(=Zc+=Zb)), the voltage across E is zero when M in not zero.
When Zc/Zb == (=Zc/=Zb), the voltage across E is zero when M in not zero.
I used the notation Zb for the Balance impedance and I used =Zc and =Zb to mean equalZc and equalZb.
The Terminal impedance, Zterm is 370R+620R/310nF
The Network impedance, Zexch is 300R+1000R/220nF
If you use my webpage: a_artline , it can be set up to show that Zexch is about equal to 2Km of artifical line terminated bt Zterm.
So, when Line length is 2km :
Zc = Zterm
Zb = Zexch
As To get minimal sidetone, set Zb to equal Zexch which is approximatly equal to 2Km of line terminated by Zterm.
My code has:
//The terminal Figure 1: Terminal Complex Impedance Network = 370+ 620//310nf
var z_complex_z = z_abc(370, 620, 310.0e-9 , freq[c] );
//The nominal exchange input impedance is 300 Ù + 1000 Ù || 220 nF (see Figure 2).
var z_complex_znom = z_abc(300.0, 1000.0, 220.0e-9 , freq[c] );
Artificial Line - speeding up the calculations.
Artifical Line is modelled using n x 0.1km sections. The range of local lines can be represented by between 0 km and 9 km of 0.5 mm copper cable with nominal characteristics of 168 Ohm/km and 50 nF/km (attenuation at 1600 Hz of 1.7 dB/km).
100 metre section = O---[===]----O
I I
=== === 2.5nF
I I
O---[===]----O
16.8 ohm
Artifical Line is modelled by n x 0.1km sections. For 7.5km of artifical line, append 75 segments of line, this requires 75 2x2 matrix multiplications using complex numbers. On My Nascom2 this took a very long time and rounding errors on 32bit floats was considered a problem. ( See [11] and [12] )
Using the word append gets around getting muddled with "Add" and "Multiply".
We add line segments by multiplying 2x2 matrices.
We add components by multiplying 2x2 matrices. see [11] and [12]
I take liberties with notation due to using ascii text using [ ] for matrix. [seg] or seg[] means 2x2 matrix. Other people use capital letters.
seg[] = [C][R][C] [C] is: [Vin] = [ 1 0 ] [Vo] [Vi ] [ 1/jwC 1 ] [Io] w=2*Pi*freq, where Freq is in Hz. [R] is: [Vin] = [ 1 R ] [Vo] [Vi ] [ 0 1 ] [Io]
The method used here takes the segments of line, doubles the length and conditionally appends this to the end to end calculation.
This cuts down the number of matrix multiplications required.
//length is length of artificial line in km.
we model it in 0.1 sections.
a[] = 0.1km section
len = len * 10
while length > 0 {
if ( LSB of Len equals 1 ) {
append a[] onto end to end chain.
apend a[] to itself to get 0.2km section
len len div 2
}
}
//PROCEDURE lines (length : REAL);
function lines( lineLength ) {
/*
This procedure evaluates line sections for unloaded line.
The model is that of BTNR 1050
Operation is akin to long multipliction , 100 meter sections
are conditionally added
*/
var len,il,il2,mask, aar,aai,abr,abi,acr,aci,aqr,aqi ;
var len = (lineLength * 10.0)&-1; //{length is km of line}
if ( len != 0 ) { // BEGIN
il=0;
il2=1;
// multz() leaves result in r[]
// multy() leaves result in r[]
// copy r[] into a[]
aar=rar; aai=rai;
abr=rbr; abi=rbi;
acr=rcr; aci=rci;
aqr=rdr; aqi=rdi;
//init r[] = 1.0
rar=1; rai=0;
rbr=0; rbi=0;
rcr=0; rci=0;
rdr=1; rdi=0;
/*
16.8/2 ohm
100 metre section = O---[===]----O
I I
=== === 2.5nF
I I
O---[===]----O
16.8/2 ohm
*/
// r[] = identity matrix
multy(0,w*2.5E-9);
multz(16.8,0);
multy(0,w*2.5E-9);
// r[] now has 0.1km section
while ( len > 0 ) {
// Starting at the Least significant bit of line length, conditionally add a section of line.
len = len & -1;
/*
{ original Pascal used. It used a way to get teh LSB by using integer DIV }
WHILE len > 0 DO
BEGIN
IF (len-2*(len DIV 2))=1 THEN
BEGIN
*/
// JAVA script ands 1 with len to get LSB
if ( ( len & 1 ) != 0 ) {
// conditionally add line segment to a[]
ar=aar; ai=aai;
br=abr; bi=abi;
cr=acr; ci=aci;
dr=aqr; di=aqi;
// a[] contains
aar=ar*rar-ai*rai+br*rcr-bi*rci;
aai=ar*rai+ai*rar+br*rci+bi*rcr;
abr=ar*rbr-ai*rbi+br*rdr-bi*rdi;
abi=ar*rbi+ai*rbr+br*rdi+bi*rdr;
acr=cr*rar-ci*rai+dr*rcr-di*rci;
aci=cr*rai+ci*rar+dr*rci+di*rcr;
aqr=cr*rbr-ci*rbi+dr*rdr-di*rdi;
aqi=cr*rbi+ci*rbr+dr*rdi+di*rdr;
il=il+il2
}
//r[] = r[]+r[]
multmat (rar,rai,rbr,rbi,rcr,rci,rdr,rdi);
// printABCD();
il2=il2+il2;
len= ( len / 2) ;
}
// copy a[] back into r[]
rar=aar; rai=aai;
rbr=abr; rbi=abi;
rcr=acr; rci=aci;
rdr=aqr; rdi=aqi;
}
} //END; {line}
ABCD Matrix - summary
/* 2x2 matrix - ascii text notation. [Vi]=[A B][Vo] [Ii] [C D][Io] */
Complex Numbers - summary
multiply:
/*
(ar+jai)(br+jbi) = (ar*br-ai*bi) +j(ar*bi+ai*br)
inverse:
1/(br+jbi) = (br-jbi)
--------------------
((br+jbi)*(br-jbi))
1/(br+jbi) = (br-jbi)
--------------------
( (br*br+bi*bi) +j(br*bi-bi*br) )
1/(br+jbi) = (br-jbi)
--------------------
( (br*br+bi*bi) )
*/