A Multipath Simulation
Doug Rice
24/11/2007
Sound in a rectangular room is modelled by the very simple crude model.
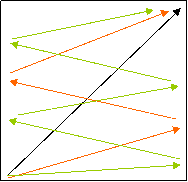
We put a loudspeaker in the corner of the room and a microphone in another corner.
There are multiple paths to the microphone, so the signals add up using vector arithmetic.
Each path has a different path length so delays the signal, and provides a phase shift.
So vector add up the signal arriving via the multiple paths and work out the magnitude of the resultant signal.
Path length = sqrt(((2n+1)*x)^2 + ((2m+1)*y)^2)
x is width of room,
y is length of room,
n are times/2, signal bounces of walls on route to microphone.
Factor is attenuation of signal via alternative path.
The Wave Equation
A solution of the wave equation is:
V = fn( t – z / v )
Where fn() is a function, t is time, z is distance and v is speed.
Let :
fn() be exp( j * 2 * pi() * f *( t - distance / velocity ) )
remember that :
exp( jx) = cos( x ) + j sin ( x )
where j = square root of - 1
The Amplitude is constant.
The phase is proportional to time or distance from the source for a given frequency and velocity.
Vector:
Real = cos( 2*pi* f*( t -pathlength/speed) )
Imag = sin( 2*pi* f*( t -pathlength/speed) )
Amplitude = SquareRoot( Real*Real + Imag*Imag )
Phase = ArcTan2( real, imaginary )
However, it is easier to do the vector addition in Cartesian co ordinatates.
TotalVector = Sum( Real ) + Sum( Imaginary )
Below are the three Phasors or Vectors for each paths above for the Room Example above.
Lets work out the resultant Phasor shown as the blue arrow below:
real
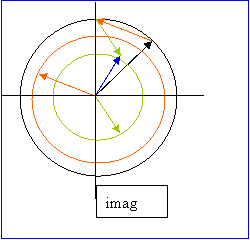
Example: Lets work out the wave equation for a Single Path
|
Parameters:- |
|
|
|
|
|
X |
2 |
|
|
|
|
Y |
3 |
|
|
|
|
speed |
300 |
|
|
|
|
n |
0 |
1 |
2 |
3 |
|
factors |
20 |
0 |
0 |
0 |
Example: two paths, equal Amplitude:-
|
Parameters:- |
|
|
|
|
|
x |
2 |
|
|
|
|
y |
3 |
|
|
|
|
speed |
300 |
|
|
|
|
n |
0 |
1 |
2 |
3 |
|
factors |
20 |
20 |
0 |
0 |
The vectors add and subtract, so we see nulls in the response.
Example: threes paths, equal Amplitude:-
|
Parameters:- |
|
|
|
|
|
x |
2 |
|
|
|
|
y |
3 |
|
|
|
|
speed |
300 |
|
|
|
|
n |
0 |
1 |
2 |
3 |
|
factors |
10 |
10 |
10 |
10 |
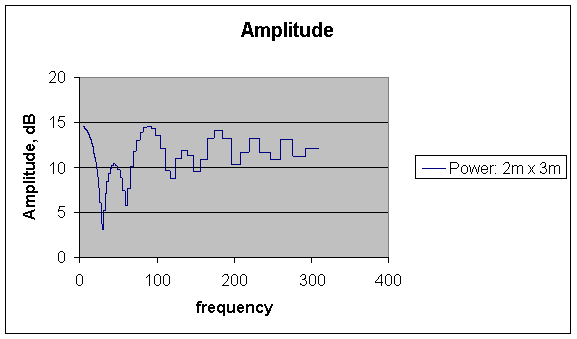
Example: four paths, equal Amplitude:-
|
Parameters:- |
|
|
|
|
|
x |
2 |
|
|
|
|
y |
3 |
|
|
|
|
speed |
300 |
|
|
|
|
n |
0 |
1 |
2 |
3 |
|
factors |
20 |
20 |
20 |
20 |
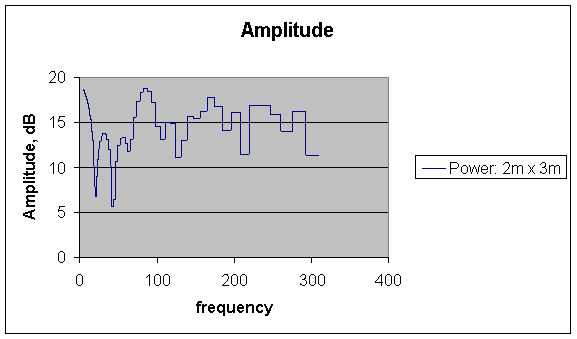
Example: two paths, shortest and longest paths, equal Amplitude:-
|
Parameters:- |
|
|
|
|
|
x |
2 |
|
|
|
|
y |
3 |
|
|
|
|
speed |
300 |
|
|
|
|
n |
0 |
1 |
2 |
3 |
|
factors |
20 |
0 |
0 |
20 |
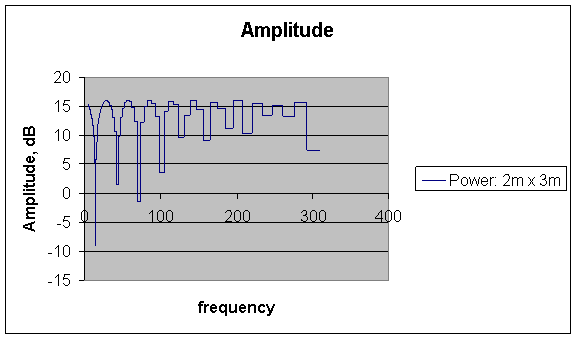
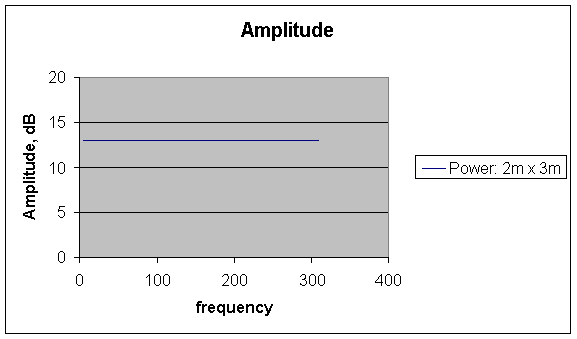
Example Compare two Rooms 2m by 2m and 2m by 3m
|
Parameters:- |
|
|
|
|
|
X |
2 |
|
|
|
|
Y |
2 |
|
|
|
|
speed |
300 |
|
|
|
|
N |
0 |
1 |
2 |
3 |
|
factors |
10 |
8 |
6 |
5 |
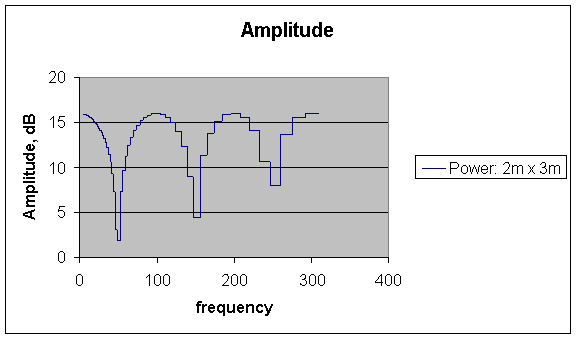
And
|
Parameters:- |
|
|
|
|
|
X |
2 |
|
|
|
|
Y |
3 |
|
|
|
|
speed |
300 |
|
|
|
|
N |
0 |
1 |
2 |
3 |
|
factors |
10 |
8 |
6 |
5 |
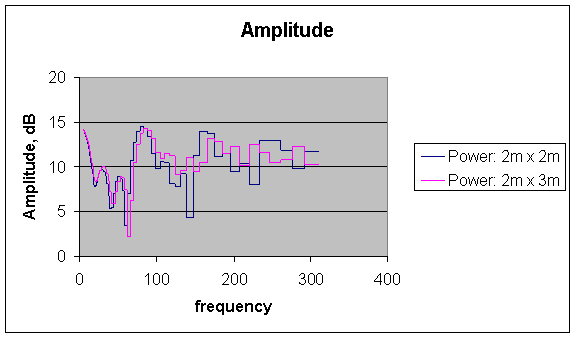
The two plots are not the same.
If you stood in the middle of the room and moved your head, you would notice the spectrum change.